👩🏻💻 Point of Today I LEARNED
📌 SQL
● 코드카타 (~80번 복습, 148번)
📌 Python
● 통계학 라이브세션 6회차 복습 (통계적 검증과 머신러닝)
● 실무에 쓰는 머신러닝 기초 4강(릿지,라쏘 회귀), 5강(분류)

인생은 존버다.
이겨내.
포기는 없숴.
1. SQL
1-1. 코드카타 제한시간 두고 풀기
1) 코드카타 148번
https://www.hackerrank.com/challenges/what-type-of-triangle/problem?isFullScreen=true
포인트. case when의 순서
select
case when a+b<=c or b+c<=a or a+c<=b then 'Not A Triangle'
when a=b and b=c and a=c then 'Equilateral'
when a=b or b=c or a=c then 'Isosceles'
when a <> b and b <> c and a<>c then 'Scalene'
end
from TRIANGLES
- 범위가 좁은 것부터 시작해야 한다. 처음 조건이 True이면 아래는 체크하지도 않고 끝남.
2. Python
2-1. 통계학 라이브세션 6회차 복습
1) 통계적 가설검정 vs 머신러닝
- 상호보완적
- 머신러닝 모델의 피처 선택에서 유의미한 피처를 찾기 위해 사전에 통계적 가설검정을 통해 확인
- 통계적 가설검정은 변수 간 독립성을 가정하고 둘의 상관성을 검증하지만, 머신러닝은 가정 없이 그냥 데이터에 맡겨서 어떤 패턴이나 상관성이 있는지 직접 학습한다. 관계가 있으면 알아서 학습. 즉, 머신러닝은 복잡한 상관관계나 비선형 관계를 쉽게 다룰 수 있다.
2) 지도학습 vs 비지도학습
- 목표
- 지도: 새로운 데이터의 결과값 예측/분류
- 비지도 : 많은 양의 새로운 데이터에 대한 통찰력
- 모델 종류
- 지도
- 선형회귀
- 로지스틱 회귀
- SVM
- KNN (최근접 이웃)
- 의사결정 트리 - 랜덤 포레스트
- 비지도
- 클러스터링(군집)
- K-means 클러스터링
- 주성분 분석(PCA)
- 지도
2-2. 실무에 쓰는 머신러닝 기초 4강, 5강
1) 고급회귀
- 회귀계수를 너무 크게 만들지 않기 위해 패널티를 주는 방식의 회귀 쓸데 없이 영향력 큰 변수 자제 시켜
- 패널티 주는 방식에 따라
- 릿지 회귀 (Ridge)
- L2 정규화 (제곱합)
- 계수 작게 줄이기 (완전히 제거는 아님)
- 라쏘 회귀(Lasso)
- L1 정규화 (절대값 합)
- 중요하지 않은 변수는 아예 0으로 만들어서 변수 제거 ➜ 변수 선택 효과
- 릿지 회귀 (Ridge)
- ElasticNet : Ridge + Lasso 혼합 ➜ 릿지의 안정성 효과 + 라쏘의 변수 선택 효과
2) 지도학습 - 분류
- 데이터에 이미 정답값(레이블)이 있고, 이를 학습한 후 어떤 라벨에 속하는지 예측하는 기법
2-1) 주요 모델
로지스틱 회귀
- 선형 회귀와 같은 수식을 사용하지만, 결과를 확률값으로 예측해서 특정 기준보다 낮으면 0 아니면 1로 반환
- 분류 뿐만 아니라 각 확률값까지 확인 가능해서 세심한 해석 가능
- 예) 0으로 분류됐지만 0.4이네. 아예 낮진 않구나.
- 장점
- 회귀계수 확인 가능해서 변수별 영향력의 크기 파악 가능
- 단순해서 과적합 방지 기능
- 단점
- 복잡한 비선형 패턴 학습에 한계 있음
- 불균형 데이터에 민감
- 이상치 민감
SVM(Support Vector Machine)

- 레이블을 나누는 기준(경계)을 찾는데, 두 레이블이 최대한 떨어져 있도록 찾는 기법
- 주요 개념
- 초평면 : 그 기준 (2D에서는 경계선) / 결정경계
- 서포트 벡터 : 초평면에 가장 가가운 데이터 포인트들
- 마진 : 초평면과 서포트 벡터 사이의 거리
- 장점
- 복잡한 비선형에서도 사용 가능 (커널 트릭->하이퍼파라미터 사용)
- 마진 최대화하면 일반화 잘 됨
- 메모리 사용이 효율적
- 과적합 방지 기능
- 단점
- 왜 이런 결과가 나왔는지 해석 어려움
- 하이퍼 파라미터(C, kurnel, gamma) 사용가능하지만 그만큼 튜닝 비용 큼
- 대규모 데이터셋에서는 학습 속도 저하
K-NN(K-최근접 이웃)
- 가장 근접한 데이터들의 특징을 통해 카테고리 분류 (거리기반 판단)
- 이웃들의 클래스 다수결로 예측
- 학습 자체는 간단하지만 복잡하고 대규모 데이터셋에서는 예측 속도 저하 (전체 데이터를 다 계산/저장하기 때문에)
- 표준화 필수
- K값은 보통 데이터셋 크기의 제곱근 정도로 시작
나이브 베이즈(Naive Bayes)
- 통계적 가정 (독립성)이 깔려 있기 때문에 계산이 빠름
신경망(MLP) 또는 딥러닝 모델
- 복잡하지만 대규모 데이터셋에서 확실한 강점
2-2) 모델 평가 방법
① 손실함수
- 모델의 예측 확률을 실제 정답과 비교해서 얼마나 차이나는지를 수치로 표현한 것 (잘못된 분류의 수치적인 손실값)
- 정답 클래스의 확률을 얼마나 정확하게 예측했어? (예측의 정확도)
- ☞ 올바르게 분류했더라도 적은 확률로 예측한거라면 성능이 좋다고 하기 어렵다. 이를 위해서 사용하는 평가 지표
- 회귀 모델의 손실함수는 MSE,MAE / 분류 모델의 손실함수는? ▼▼▼
- Cross Entropy(다중) / Binary Cross Entropy(이진)
- 예측 확률이 실제 레이블과 얼마나 차이가 나는지 확인
- 낮을수록 잘 한 예측
- Hinge Loss
- SVM 에서 많이 사용 (데이터 간의 공간(마진)을 고려해서 오분류된 샘플에 패널티 부여)
- Cross Entropy(다중) / Binary Cross Entropy(이진)
② 혼동 행렬 ⭐️⭐️⭐️⭐️⭐️
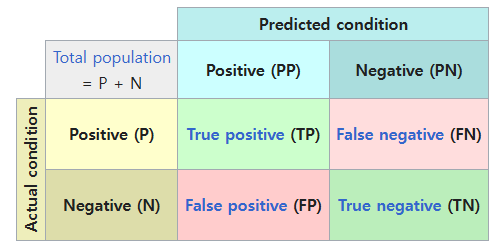
- 실제값과 예측값의 관계를 행렬 형태로 나타낸 것
- 4분할로 볼 수 있기 때문에 클래스 불균형 상태에서도 정확하고 세밀한 성능 평가 가능⭐️
- 1종 오류, 2종 오류 파악 가능
- 히트맵으로 시각화해서 평가 지표 확인 가능
- Accuracy(정확도) : 전체 데이터 중 맞힌 비율 ☞ 불균형에 약함
- Precision(정밀도) : 예측값 positive 중 실제값 positive 한 비율 ☞ False Positive가 치명적 / 예측 정확도가 중요 (스팸)
- Recall(재현율) : 실제값 positive 중 예측값 positive 한 비율 ☞ False Negative가 치명적 / 실제를 놓치지 않는 것이 중요 (질병 진단)
- F1-scroe : Precision와 Recall의 조화 평균 ☞ 둘 다 중요할 때 종합적으로 평가
- 목표에 따라 중요한 지표가 다를 수 있으나, 확실한 건 정확도 하나로 평가하면 안 된다는 거.
③ ROC 곡선, AUC(Area Under the Curve)
- ROC 곡선
- 임계값(Threshold) 변화에 따른 TPR(True Positive Rate)과 FPR(False Positive Rate)의 관계를 시각화한 곡선
- 임계값 : 모델이 어떤 확률로 positive라고 예측할지 결정하는 기준점
- 예시) 로지스틱 회귀의 확률값 기준 / SVM의 초평면(경계선)
- 이걸 0~1 사이 값으로 변화시키면서 tpr, fpr을 측정
- TPR(True Positive Rate)
- 실제 양성을 '양성'으로 옳게 예측한 비율 (TP / TP + FN)
- = Recall(재현율), 민감도
- 1에 가까울수록 좋음
- FPR(False Positive Rate)
- 실제 음성을 '양성'으로 잘못 예측한 비율 (FP / FP + TN)
- 0에 가까울수록 좋음
- 임계값(Threshold) 변화에 따른 TPR(True Positive Rate)과 FPR(False Positive Rate)의 관계를 시각화한 곡선
- AUC(Area Under the Curve)
- ROC 곡선 아래 면적
- 양성/음성 구분을 얼마나 잘 판별했는지 평가 (not 정확도)
- '양성'클래스일 가능성을 얼마나 잘 판별했어?
- 1에 가까울수록 양성/음성을 잘 구별했고, 0.5에 가까울수록 무작위라는 의미
- = 곡선이 좌상단에 가까울수록 좋은 모델 (= FPR은 낮고, TPR이 높다) / 랜덤선보다 낮으면 매우 심각
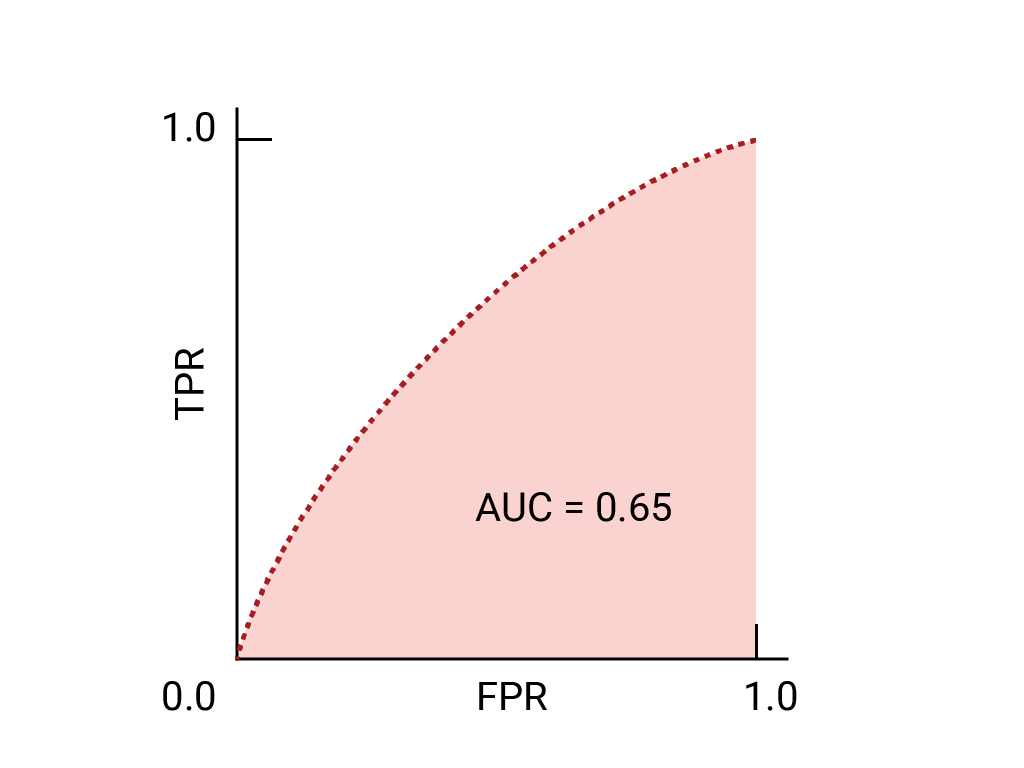
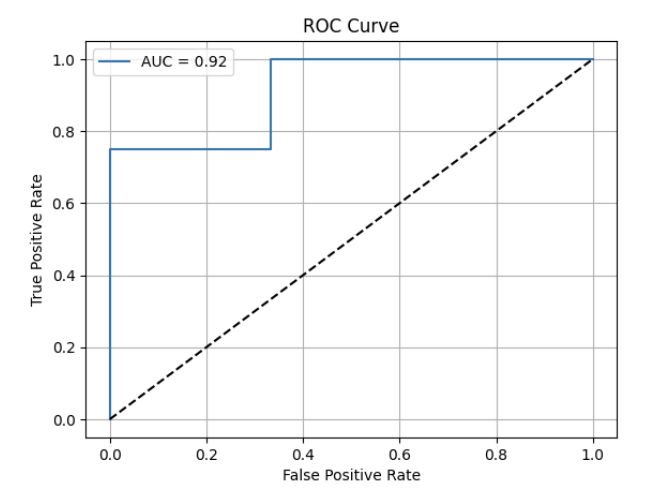
✅ 정리
1. 단순히 예측 결과로 성능 평가하고싶으면
y_pred = model.predict(X_test) # ➜ 클래스 예측 cunfusion_metrix(y_test, y_pred) # ➜ 혼동행렬 만들고 시각화 classificatioin_report(y_test, y_pred) # ➜ 바로 평가 지표 확인2. ROC-AUC 사용해서 확률 기반 정밀 평가 하고싶으면 (이진분류일 때만)
y_proba = model.predict_proba(X_test)[:,1] # ➜ 양성으로 예측할 확률값 파악 fpr, tpr, threshold = roc_curve(y_test, y_proba) # ➜ roc 곡선 시각화 준비 auc_score = roc_auc_score(y_test, y_proba) # ➜ auc score 파악
* 다중분류일 경우 추가 처리 필요from sklearn.metrics import roc_auc_score from sklearn.preprocessing import label_binarize # 예: 클래스가 0, 1, 2인 경우 y_test_binarized = label_binarize(y_test, classes=[0, 1, 2]) # ovr을 위한 원핫인코딩(이진화) y_pred_proba = model.predict_proba(X_test) roc_auc_score( y_test_binarized, y_pred_proba, average='macro', multi_class='ovr') # average 종류 # 1.macro: 단순평균 # 2.weighted: 비율 가중 평균(불균형 반영) # 3.micro: 전체 데이터를 하나의 이진문제로 보고 계산
1) roc curve를 각 클래스마다 만들기 위해 One-vs-Rest 방식 사용 ➜ 각 roc-auc들의 평균 계산
예시) 사람, 개, 고양이를 분류하는 문제일 경우 → 사람 vs 나머지, 개 vs 나머지, 고양이 vs 나머지
2) One-vs-Rest을 위해 라벨 이진화시키기(label_binarize)
- 실습
✅ 코딩 순서
1. 데이터 로딩 및 분할 train_test_split
2. 모델 학습 / 예측 LogisticRegression(max_iter=500)
3. 혼동행렬 시각화 ConfusionMatrixDisplay
4. 예측 기반 성능평가 (정확도, 리포트) accuracy_score, classification_report
5. 다중분류 AUC 평가 label_binarize, predict_proba, roc_auc_score
# 다중분류 최종 실습 문제
import pandas as pd
import numpy as np
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score, confusion_matrix, accuracy_score, classification_report
from sklearn.preprocessing import label_binarize
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
wine = load_wine()
X = wine.data
y = wine.target
X_train, X_test, Y_train, Y_test = train_test_split(X,y, test_size=0.2, random_state=42, stratify=y)
model = LogisticRegression(max_iter=500)
model.fit(X_train, Y_train)
y_pred1 = model.predict(X_test)
# 예측결과 기반 평가
cm1 = confusion_matrix(Y_test, y_pred1)
disp1 = ConfusionMatrixDisplay(cm1)
disp1.plot()
print(f'정확도:', accuracy_score(Y_test, y_pred1))
print(classification_report(Y_test, y_pred1, target_names=wine.target_names))
# 다중분류 확률 정밀 기반 평가
y_test_binarized = label_binarize(Y_test, classes=np.unique(y))
y_prob1 = model.predict_proba(X_test)
# ROC Curve 계산 및 시각화
fprs, tprs, roc_auc = {},{},{}
for i in range(len(classes)):
fprs[i], tprs[i], _ = roc_curve(y_test_binarized[:, i], y_prob1[:, i])
roc_auc[i] = auc(fprs[i], tprs[i])
for i in range(len(classes)):
plt.plot(fprs[i], tprs[i], label=f'Class_{i} AUC: {roc_auc[i]:.2f}')
plt.figure()
plt.plot([0, 1], [0, 1], linestyle='--') #랜덤 분류선(대각선)->이 선을 기준으로 roc곡선에 대해 평가할 수 있어서 직관적임
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()
auc_score = roc_auc_score(y_test_binarized, y_prob1, average='macro', multi_class='ovr')
print(f'다중분류 auc점수: {auc_score:.4f}') # 의미: '각 클래스에 대해' 얼마나 잘 예측했는지의 평균'데이터 분석' 카테고리의 다른 글
| [250416] 이상탐지, 회귀 (0) | 2025.04.16 |
|---|---|
| [250415] 알고리즘 선택가이드, 앙상블, 하이퍼파라미터 튜닝 (0) | 2025.04.15 |
| [250411] ⭐️ 분석 흐름 정리 ⭐️, 트리기반모델 (1) | 2025.04.11 |
| [250410] 윈도우 함수에서의 group by, 재귀문, having, on절에 case when / 유형별 통계검증법, 상관계수 분류 (0) | 2025.04.10 |
| [250409] 로지스틱회귀, 선형회귀모델의 성능평가, 파이프라인 (0) | 2025.04.09 |